This is my first post about my new hobby, smart homes in general and specifically HomeMatic, and it’s already quite a technical one: solving the AES authentication problem with the new HM-SEC-SD-2 smoke detectors. The detectors use cryptographic authentication between them so that not every grumpy neighbour can activate the alarm. This is good, but also a problem when you want to activate the alarm yourself, as part of a burglary system for example.
The main tip came from Michael Gernoth, who mentioned that the CCU2 software used to contain a function called performCBCAuthentification, which sounded like it could fit the given scenario. Fortunately reverse engineering is something I’m usually pretty good at, so I set out to have a look. Reverse engineering binary code is somewhat akin to assembling ground coffee back into beans. Challenging but also satisfying when it works. The tool of choice is a somewhat expensive tool called IDA which my employer fortunately bought for me to do my job. Unfortunately not the very expensive version that can actually output C-like code, just the disassembler one, but we can work with that 😉
From ground coffee…
On the high level overview the function in question looks like this:
Which is actually not too bad. Somewhat regular and not too much code overall. Zooming into one part looks like this:
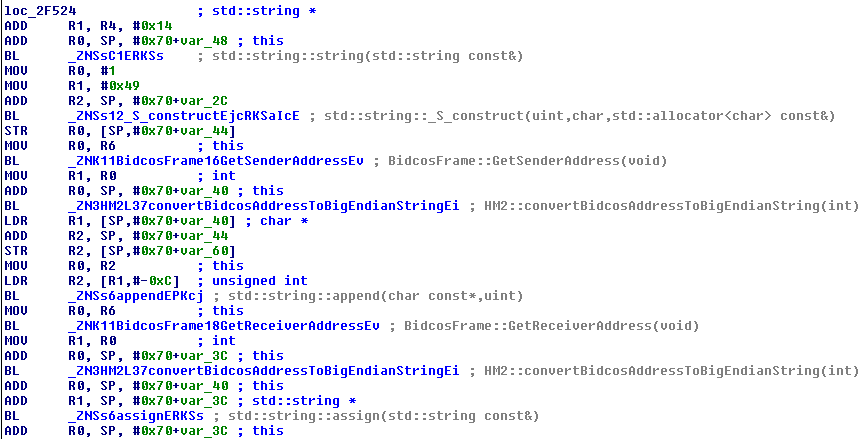
This may look wild to the untrained eye but is actually great news: one one hand, it’s ARM assembler, which I have never read before and also, it’s C++, which is a pain to read in assembler, but on the other hand we see that IDA found many symbols and that most function calls actually have names. This is like winning the lottery! One function call in particular shows what it means to have C++ code at hand:
BL _ZNSt8_Rb_treeIiSt4pairIKiSsESt10_Select1stIS2_ESt4lessIiESaIS2_EE17_M_insert_unique_ESt23_Rb_tree_const_iteratorIS2_ERKS2_ ; std::_Rb_tree<int,std::pair<int const,std::string>,std::_Select1st<std::pair<int const,std::string>>,std::less<int>,std::allocator<std::pair<int const,std::string>>>::_M_insert_unique_(std::_Rb_tree_const_iterator<std::pair<int const,std::string>>,std::pair<int const,std::string> const&)
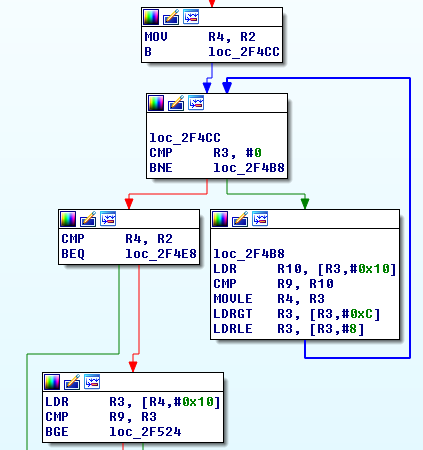
Everything clear now? Thought so. Unfortunately our newly found fortune doesn’t cover variables and object properties, so parts like the following look a lot easier visually but without any clue what the data is, is a lot harder to analyze:
It looks like it’s traversing a doubly linked list in search of the encryption key, but I haven’t analyzed this part of the code 100% and probably don’t need to.
… to the beans…
In the first step I tediously transcribed the code I’ve seen back into something somewhat resembling source code. By hand…
DWORD __cdecl StructuredFrame::GetIntValue(int offset, int, int size, int *result)
{
[...]
}
// BidCosFrame inherits from StructuredFrame
int BidcosFrame::GetSenderAddress(void)
{
int result;
if (!StructuredFrame::GetIntValue(3, 0, 3, &result)) return -1;
return result;
}
int BidcosFrame::GetReceiverAddress(void)
{
int result;
if (!StructuredFrame::GetIntValue(6, 0, 3, &result)) return -1;
return result;
}
// HM2 probably inherits from std::string
DWORD __fastcall HM2::convertBidcosAddressToBigEndianString(int x)
{
byte tmp[4];
tmp[2] = x >>; 16;
tmp[1] = x >>; 8;
tmp[0] = x;
this.append(tmp, 3);
}
DWORD __fastcall RFChannel::performCBCAuthentification(BidcosFrame *Frame)
{
int tmp;
frameSize = Frame.GetSize();
if (frameSize <= 14) return 0;
Frame.GetIntValue(frameSize - 6, 0, 1, 0, &tmp);
iv = (byte)tmp;
Frame.GetIntValue(frameSize - 5, 0, 1, 0, &tmp);
iv = iv << 8 + (byte)tmp;
Frame.GetIntValue(0, 0, 1, 0, &tmp);
iv = iv << 8 + (byte)tmp;
if (iv <= this->AesCbcCounter) return 0;
// Get Key from RFManager... somehow
keyStr = new std::string(...key...);
ivStr = new std::string(1, '\49', std::allocator);
ivStr.append(convertBidCosAddressToBigEndianString(Frame.GetSenderAddress()));
ivStr.append(convertBidCosAddressToBigEndianString(Frame.GetReceiverAddress()));
ivStr.append(convertBidCosAddressToBigEndianString(iv);
ivStr.append(5, '\0');
ivStr.append(1, '\5');
AES_init_key(keyStr);
byte *block1 = new byte[16];
AES_encrypt_block(ivStr, block1);
str2 = new std::string();
str2.append(Frame.GetByteData(0), 1); // Count
str2.append(Frame.GetByteData(1), 1); // Flags
size = Frame.GetSize() - 15;
if (size < 0) return 0;
if (size >= 14) size = 14;
if (size != 0) {
str2.append(GetDataByte(9), 1); // Channel
r5 = size + 9; // FrameSize - 6
r4 = 10;
if (r5 != r4) {
if ((size - 1) & 1 != 0) {
str2.append(GetDataByte(r4++), 1);
}
while (r4 != r5) {
str2.append(GetDataByte(r4++), 1);
str2.append(GetDataByte(r4++), 1);
}
}
if (size != 14) {
str2.append(size - 14, '\0');
}
}
block1[0] ^= str2[0];
block1[1] ^= str2[1];
block1[2] ^= str2[2];
block1[3] ^= str2[3];
block1[4] ^= str2[4];
block1[5] ^= str2[5];
block1[6] ^= str2[6];
block1[7] ^= str2[7];
block1[8] ^= str2[8];
block1[9] ^= str2[9];
block1[10] ^= str2[10];
block1[11] ^= str2[11];
block1[12] ^= str2[12];
block1[13] ^= str2[13];
block1[14] ^= str2[14];
block1[15] ^= str2[15];
AES_init_key(keyString);
byte *block2 = new byte[16];
AES_encrypt_block(block1, block2);
int a = Frame.GetDataByte(frameSize - 4) ... Frame.GetDataByte(frameSize - 1);
int b = block2[12] ... block2[15];
return a == b? a: 0;
}This is not supposed to compile and there might be transcription errors or bugs in it. It’s just to get your notes in order and is certainly a lot more readable than the code we’ve started with, so we can finally deduct the algorithm from it!
… to the algorithm …
Given the example frame of:
00 01 02 030405 060708 09 0A 0B 0C 0D 0E 0F101112 01 14 41 44E347 44E347 01 01 96 00 00 03 0A802A78 | Flg | Sender Recvr | | | IV1 | Cnt Type Chn No State IV2
- Build an initialization vector containing:
- One byte with the value 49
- The sender address (3 bytes)
- The receiver address (3 bytes)
- The byte marked “IV1”
- The byte marked “IV2”
- The Cnt byte
- 5 bytes of zero
- One byte with the value 5
In our example frame this adds up to “4944e34744e347000301000000000005”.
- Encrypt this using the AES key, which results in “d064bd7e0161592f1175f1c9e822f87b”.
- Build a second frame using:
- The Cnt byte
- The Flg byte
- The Chn byte
- All bytes from field “No” up to FrameSize – 6 (just leaving out the signature and the IV bytes)
- Fill the rest up with zero so that we have 16 bytes again
This gives us “01140101960000000000000000000000”.
- XOR the result of the AES encryption with our second frame. This gives us “d170bc7f9761592f1175f1c9e822f87b”
- AES encode the result again. This gives us “d051f2c911e8cb716057a89d0a802a78“
- Lo and behold, the last 4 bytes match the signature in our example frame! Perfect
… to the end
The CCU2 code only contains the routine to check a signature, not to generate one. So at this stage it’s unknown to me why the two IV bytes have the value they have, as I don’t own the hardware yet nor was I given any more example frames to work with. Maybe they can be chosen freely, maybe they are counted up. In any case, the remaining work should be fairly easy to do in comparison. Hope I could help!
Great work!
Thanks! Glad it was of interest to you 🙂